İnformatika üzrə Respublika Olimpiadasının II rayon turunun məsələləri (2012/2013-ci dərs ili)
Məsələ 1(10 xal)
Verilmiş sözdə STUDENT sözündə olan bütün hərfləri təmizləyin.
Giriş verilənlər: Giriş verilənləri ingilis dili əlifbasının 3-dən az və 20-dən çox olmamaqla böyük hərflərindən ibarət sözdür.
Çıxış verilənləri: Çıxış verilənləri girişdə verilən sözdə STUDENT sözünə daxil olan bütün hərfləri təmizlədikdən sonra alınan sözdür.
|
Nümunə |
Giriş verilənləri |
Çıxış verilənləri |
|
1 |
DAY |
AY |
|
2 |
DUTY |
Y |
Həlli:
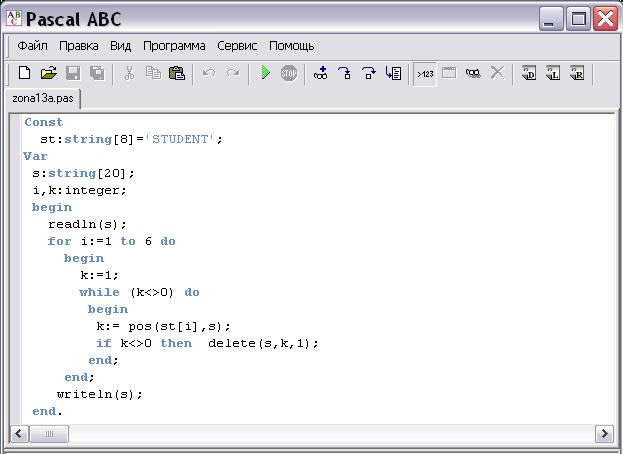
Məsələ 2(15 xal).
Respublika Olimpiadasında yeni qaydalara görə 8 məsələ təklif ediləcək. Hər bir Olimpiada iştirakçısı istənilən məsələləri həll edə bilər, lakin hər bir iştirakçının yekun xalları cəmi ən yüksək xal almış 5 məsələ üzrə qiymətləndirilir. Hər məsələ üzrə toplanmış xallara görə iştirakçının yekun xalını və xalları yekun qiymətləndirməyə daxil olan məsələlərin nömrələrini müəyyənləşdirən proqramı yazın. Hər məsələ üzrə toplanmış xallar müxtəlifdir.
Giriş verilənlər: Bir sətirdə aralarında boşluq işarəsi olmaqla iştirakçının hər bir məsələ üzrə aldığı xallar olan 8 tam ədəd yerləşir. i-ci ədəd i-ci məsələ üzrə toplanmış xaldır.
|
Nümunə |
Giriş verilənləri |
Çıxış verilənləri |
|
1 |
20 30 50 48 33 66 0 64 |
261 3 4 5 6 8 |
|
2 |
20 0 50 80 77 110 56 48 |
373 3 4 5 6 7 |
Çıxış verilənləri: Çıxış verilənləri iki sətirdən ibarətdir. Birinci sətirdə iştirakçının cəmi topladığı maksimum xal (5 ən yaxşı həll üzrə) yerləşir. İkinci sətirdə xalları yekun qiymətləndirmədə nəzərə alınan məsələlərin nömrələri aralarında boşluq işarəsi olmaqla artma ardıcıllığı ilə verilir.
Həlli:
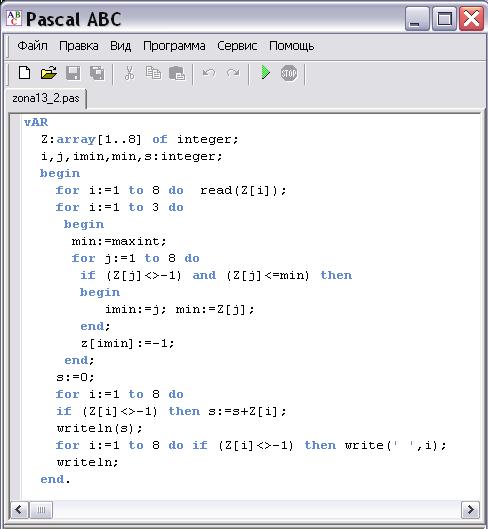
Məsələ 3(15 xal).
Məmməd müstəvi üzərində elə 4 nöqtə seçməlidir ki, onlar tərəfləri koordinat oxlarına paralel olan düzbucaqlının təpə nöqtələri olsun. O, artıq üç nöqtə seçib. Dördüncü nöqtəni müəyyənləşdirməkdə ona kömək edin.
Giriş verilənlər: Üç sətirdə aralarında bir boşluq işarəsi olmaqla düzbucaqlının seçilmış təpə nöqtələrinin (X,Y) koordinatları yerləşir. Hər bir təpə nöqtəsi ayrıca sətirdədir. Bütün ədədlər tamdır və 1-lə 1000 arasında yerləşir.
Çıxış verilənləri: Bir sətirdə aralarında bir boşluq işarəsi olmaqla düzbucaqlının dördüncü təpə nöqtəsinin koordinatları olan iki tam ədəd.
|
Nümunə |
Giriş verilənləri |
Çıxış verilənləri |
|
1 |
5 5 5 7 7 5 |
7 7 |
|
2 |
30 20 10 10 10 20 |
30 10 |
Həlli:
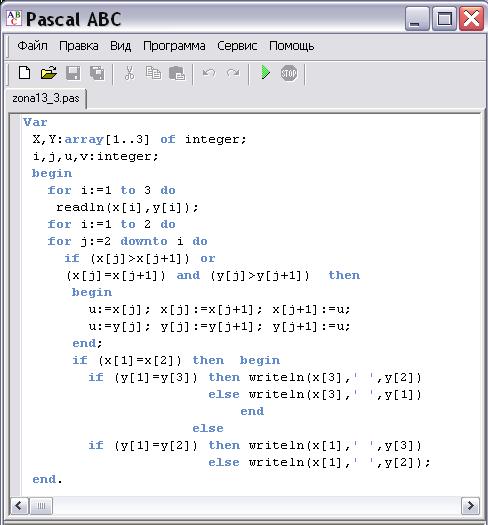
Məsələ 4(15 xal).
Məmmədin atası Yeni il bayramı üçün kvadrat tort sifariş verdi və bu tortu onun tərəflərinə paralel düz xətlərlə maksimum sayda neçə hissəyə kəsməyin mümkünlüyünü hesablamağı Məmmədə tapşırdı. Hər bir xətt tortu tam kəsib bölür.
Giriş verilənlər: Bir sətirdə bir natural N (1<=N<=100) ədədi.
Çıxış verilənləri: Tortu kəsib bölmək mümkün olan hissələrin maksimum sayı olan bir ədəd.
|
Nümunə |
Giriş verilənləri |
Çıxış verilənləri |
|
1 |
1 |
2 |
|
2 |
3 |
6 |
Məsələ 5(15 xal).
Məmməd ədədi silsilə əmələ gətirən 4 ədəd seçdi, başqa sözlə, elə 4 ədəd ki, əgər onları artma sırası ilə düzsək istənilən iki qonşu ədədlər arasındakı fərq həmişə eyni olacaq. Həmişə olduğu kimi, Məmməd ədədlərdən birini itirdi və yadına da sala bilmir. Bu dördüncü ədədi tapmaqda Məmmədə kömək edin.
Giriş verilənlər: Bir sətirdə boşluq işarəsi ilə ayrılmış üç natural ədəd. Hər bir ədəd 100-ü aşmır.
Çıxış verilənləri: Verilmiş üç ədədlə ədədi silsilə əmələ gətirən bir ədəd. Əgər belə ədədlər birdən çoxdursa, onda onlardan ən böyüyü seçilir.
|
Nümunə |
Giriş verilənləri |
Çıxış verilənləri |
|
1 |
4 6 8 |
10 |
|
2 |
10 1 4 |
7 |
1. İkinin quvvətləri.
N ədədi daxil edilir (1≤ N ≤ 106 ). Həmin ədəd ikinin hər hansı qüvvətidirsə YES, əks halda NO sözünü çap edən proqram tərtib et.
2. N, M və K üç natural ədəd daxil edilir. N-dən M-dək (M özü də daxil olmaqla) olan ədədlərin içərisindən rəqəmlərinin cəmi K-ya qalıqsız bölünən ədədlərin sayını tapın.
|
Giriş |
Çıxış |
|
1 100 3 10 22 4 |
33 3 |
3. Dovşan N uzunluqda yolda yalnız irəliyə tullana bilir. Dovşanın tullanış məsafəsinin uzunluğu K-dan(1≤ K, N≤ 100)çox deyildir. Dovşanın bütün yolu əvvəldən axıradək tullanaraq keçməsi üçün müxtəlif üsulların sayını göstərən ədədi tapın.
Məsələn, N=3, K=2 üçün dovşanın mümkün tullanışları 1,1,1; 1,2; 2,1.
Bu halda cavab 3 olacaq.
Giriş N və K ədədləridir.
4. A+B=C tənliyi verilmişdir. Belə ki, burada A, b və C onluq yazılışında bəzi rəqəmləri ? işarəsi ilə əvəz olunmuş mənfi olmayan təm ədədlərdir.
?2 + 34 = 4? belə tənliyə bir nümunədir. ? işarəsinin yerinə elə rəqəmləri qoymaq tələb olunur ki, bu tənlik doğru bərabərliyi çevrilsin, ya da müəyyən edilsin ki, belə bərabərlik mümkün deyil. Mümkün həllərdən yalnız birini tapın.
Giriş verilənlər: uzunluğu 40 simvoldan çox olmayan və boşluq işarəsi daxil olmadan tənlikdir.










